A number system in computer is a method of representing numbers using a set of digits or symbols in a consistent way, which enables computers to store, process, and communicate data efficiently. The value of each digit in a number depends on the digit itself, its position in the number, and the base (or radix) of the number system
Table of Contents
What Is a Number System?
Number System in computer defines a set of values used to represent quantity.
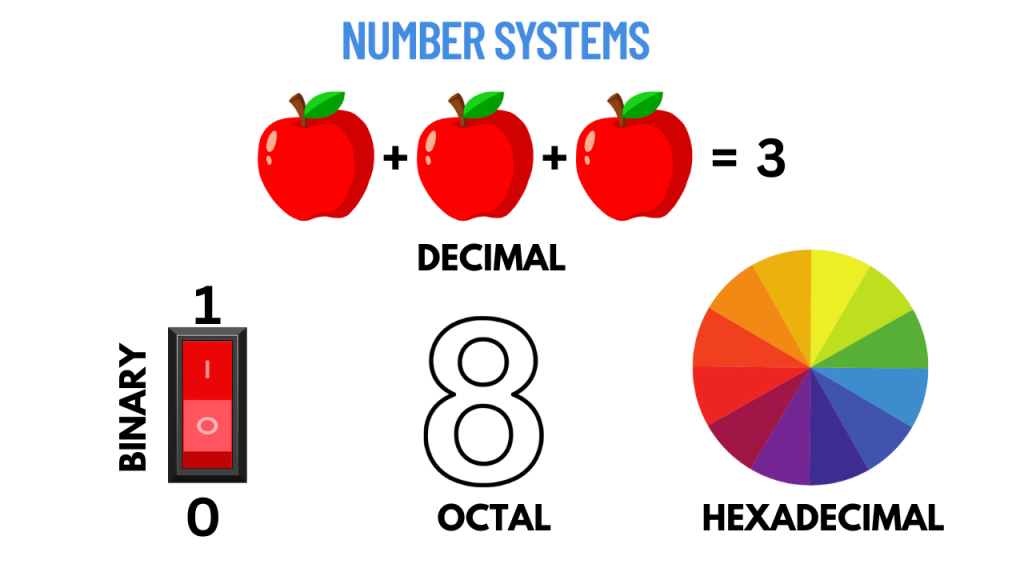
A number system is a set of rules for representing numbers. The base (also called radix, often written as r) tells us how many unique digits we have. For example, in the decimal system, the base is 10, so we have digits from 0 to 9. In binary, the base is 2, so we only have 0 and 1.
| Name | Base | Digits/ Symbols |
| Binary | 2 | 0,1 |
| Octal | 8 | 0-7 |
| Decimal | 10 | 0-9 |
| Duodecimal | 12 | 0-9, A, B |
| Hexadecimal | 16 | 0-9, A-F |
You might notice that as the base increases, the set of digits expands. For example, in hexadecimal (base 16), we use the letters A–F to represent the values 10–15.
Understanding the Base and Radix
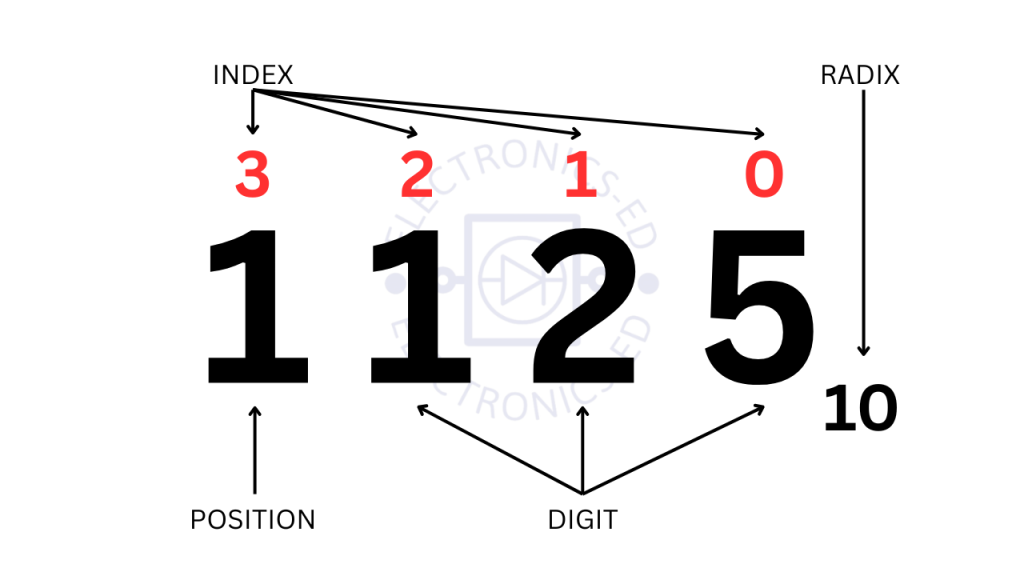
The base is the foundation of any number system. It tells us how many unique digits we have. The digits always start at 0 and go up to one less than the base. For example:
- Binary: base 2 → digits 0 and 1
- Octal: base 8 → digits 0 through 7
- Decimal: base 10 → digits 0 to 9
- Duodecimal: base 12 → digits 0–9, A (for 10), B (for 11)
- Hexadecimal: base 16 → digits 0–9, A–F (where F = 15)
If you know the base, you can always figure out the possible digits.
Weighted and Unweighted Codes
Not all number systems are created equal. Some are weighted, meaning each digit’s position has a specific value or weight. The decimal system is weighted. For example, the number 7,392 can be written as:
7,392 = 7 × 10³ + 3 × 10² + 9 × 10¹ + 2 × 10⁰Each digit’s value depends on its position. The weight of each position is a power of 10. This is why we call it a weighted number system.
On the other hand, unweighted codes don’t assign values based on position. Examples include Gray code and Excess-3 code. These are used in special applications where position doesn’t matter as much.
Examples
- Weighted Codes:
- Decimal
- Binary
- Octal
- Binary Coded Decimal (BCD)
- Unweighted Codes:
- Gray code
- Excess-3 code
Comparing Decimal, Binary, Octal, and Hexadecimal
Let’s take a number—say, 7,392—and see how it’s represented in different systems.
- Decimal: 7,392 (four digits)
- Binary: 1110011100000 (thirteen bits)
- Octal: 16,340 (five digits)
- Hexadecimal: 1CE0 (four digits)
Notice how the number of digits changes as the base increases. The higher the base, the fewer digits you need to represent the same quantity. This is a key insight: as the base goes up, the number of digits goes down.
Why Does This Matter?
In computers, binary is the foundation. But binary numbers can get very long. That’s why we often use hexadecimal (base 16) or octal (base 8) as shorthand. For example, a binary number like 11010110 can be written as D6 in hexadecimal, which is much easier to read and work with.
Practical Implications
Understanding number systems is crucial for:
- Programming: You’ll often need to convert between decimal, binary, and hexadecimal.
- Electronics: Digital circuits use binary, but engineers use hexadecimal for simplicity.
- Data Representation: All data in computers is stored as binary, but it’s often displayed as decimal or hexadecimal.
Quick Reference Table
Here’s a handy table for converting between number systems for the number 15:
| Base | Name | Representation |
|---|---|---|
| 2 | Binary | 1111 |
| 8 | Octal | 17 |
| 10 | Decimal | 15 |
| 16 | Hexadecimal | F |
Summary
- Number systems are everywhere. From counting money to programming computers, you’re always using some kind of number system.
- The base defines the system. It tells you how many unique digits you have.
- Weighted vs. unweighted. Some systems assign value based on position; others don’t.
- Higher base = fewer digits. To represent the same quantity, you need fewer digits as the base increases.
Conclusion
Learning about number system in computer opened my eyes to how computers process information. It’s amazing to think that all the complex data, images, and programs we use every day are ultimately just collections of 0s and 1s. But thanks to different number systems, we can work with these numbers in ways that make sense to us.
If you’re interested in technology, engineering, or just want to understand how the digital world works, mastering number systems is a great first step.
FAQ: Frequently Asked Questions
1. What is a number system?
A number system is a method for representing quantities using a set of digits and a base. The most common is the decimal system (base 10), but computers use binary (base 2), and programmers often use hexadecimal (base 16).
2. Why do computers use binary?
Number system in computers use binary because electronic circuits can easily represent two states: on (1) and off (0).
3. What is the difference between weighted and unweighted number systems?
In weighted systems, each digit’s position has a specific value (like the ones, tens, hundreds in decimal). In unweighted systems, the position doesn’t determine the value.
4. How do you convert between number systems?
You can convert by dividing the number by the new base and keeping track of the remainders. For example, to convert decimal to binary, keep dividing by 2 and note the remainders.
5. What is hexadecimal used for?
Hexadecimal is used in computing to represent binary data in a compact, human-readable form. It’s especially common in programming and debugging.


