Mass Action Law in Semiconductor | Electronic Devices

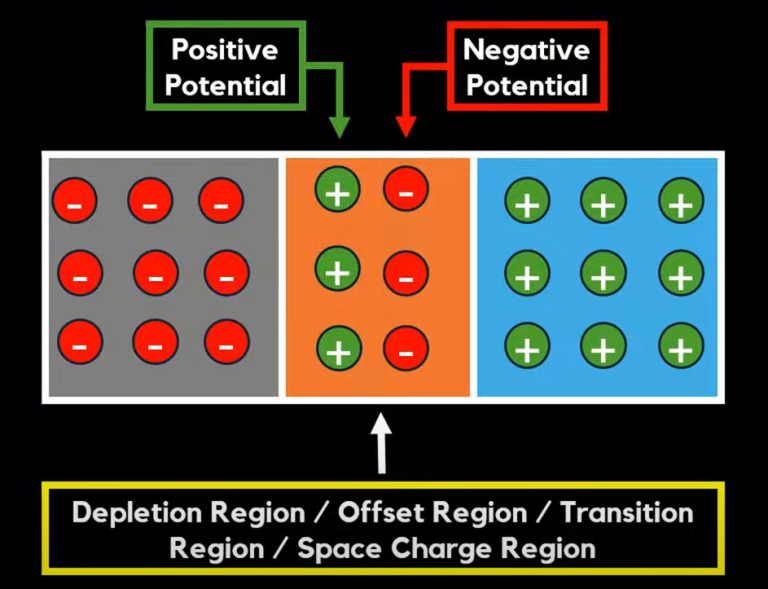
The law of mass action states that, at a fixed temperature, the product of the number of electrons and holes in a semiconductor remains constant-regardless of doping.
This law applies to both intrinsic and extrinsic (n-type and p-type) semiconductors, provided the material is not degenerate.
Understanding this law is essential for analyzing carrier concentrations and predicting device behavior in electronic circuits.

If you want a quick visual explanation, check out this video:

What Is the Law of Mass Action in Semiconductors?

Let me break it down as simply as possible. The law of mass action is a fundamental rule in semiconductor physics. It says that the product of the number of free electrons in the conduction band ( $n$ ) and the number of holes in the valence band ( $p$ ) is always constant at a given temperature. This constant is the square of the intrinsic carrier concentration ( $n_{i}^{2}$ ).

So, the equation looks like this:

$n \times p = n_{i}^{2}$

Here’s what those terms mean:

n: Number of free electrons in the conduction band
p: Number of holes in the valence band
n_i: Intrinsic carrier concentration (the number of electrons or holes in a pure, undoped semiconductor at thermal equilibrium)

This law is true whether you’re dealing with a pure (intrinsic) semiconductor or a doped (extrinsic) one, as long as the temperature stays the same and the material isn’t so heavily doped that it becomes degenerate.

Why Does the Law Matter?

Understanding the law of mass action helps me predict how a semiconductor will behave when I add impurities (dope it), or when the temperature changes. It’s a powerful shortcut for calculating unknown carrier concentrations, especially in real-world devices.

Let’s say I know the electron concentration in a silicon sample at room temperature. If I also know the intrinsic carrier concentration, I can instantly calculate the hole concentration using the mass action law. This saves a lot of time and avoids complicated quantum mechanics.

How Does It Work in Intrinsic Semiconductors?

In an intrinsic (pure) semiconductor, the number of electrons equals the number of holes:

$n = p = n_{i}$

So, plugging into the law:

$n \times p = n_{i} \times n_{i} = n_{i}^{2}$

This is the baseline for everything else. At room temperature, for silicon, $n_{i}$ is about $1.5 \times 10^{10}$ per cubic centimeter. That’s not a lot compared to metals, but it’s enough to let silicon conduct electricity.

What About Extrinsic Semiconductors?

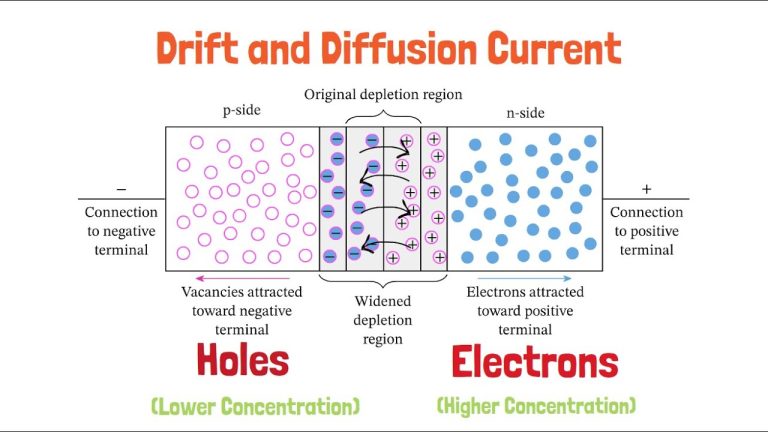
When I dope a semiconductor, I add impurities that either give up extra electrons (n-type) or create extra holes (p-type). This shifts the balance:

n-type: More electrons, fewer holes
p-type: More holes, fewer electrons

But-and this is the beauty of the law-the product $n \times p$ stays the same at a fixed temperature.

Let’s see how that looks for each type.

n-type Semiconductor

Majority carriers: Electrons ( $n$ )
Minority carriers: Holes ( $p_{n}$ )

The mass action law becomes:

$n \times p_{n} = n_{i}^{2}$

If I increase the number of electrons by doping, the number of holes must decrease so that their product remains constant.

p-type Semiconductor

Majority carriers: Holes ( $p$ )
Minority carriers: Electrons ( $n_{p}$ )

The law is:

$p \times n_{p} = n_{i}^{2}$

Again, as the number of holes rises (thanks to acceptor doping), the number of electrons drops to keep the product unchanged.

Visualizing the Relationship

Here’s a simple table to show how the numbers change:

Semiconductor Type	Majority Carrier	Minority Carrier	Mass Action Law Equation
Intrinsic	Electrons & Holes (equal)	Electrons & Holes (equal)	$n = p = n_{i}$ , $n \times p = n_{i}^{2}$
n-type	Electrons	Holes	$n \times p_{n} = n_{i}^{2}$
p-type	Holes	Electrons	$p \times n_{p} = n_{i}^{2}$

What Determines the Constant?

The constant $n_{i}^{2}$ depends on temperature and the material’s properties (like band gap). As temperature goes up, $n_{i}$ increases, so the product $n \times p$ increases too. But, for a given temperature and material, it’s fixed.

Common Questions I Get

Does the law of mass action always apply?
It works for both intrinsic and extrinsic semiconductors, as long as the material isn’t degenerate (which happens only with extremely heavy doping). In those rare cases, quantum effects take over and the law breaks down.

How does doping affect carrier concentrations?
Doping increases the majority carrier concentration and decreases the minority carrier concentration, but the product stays the same.

Why is this law useful in electronic devices?
It lets me figure out unknown carrier concentrations quickly, which is essential for designing and analyzing diodes, transistors, and integrated circuits.

Real-World Example

Suppose I have a silicon sample at room temperature ( $n_{i} = 1.5 \times 10^{10}$ cm $^{- 3}$ ). I dope it to make $n = 10^{16}$ cm $^{- 3}$ . What’s the hole concentration?

$p = \frac{n_{i}^{2}}{n} = \frac{(1.5 \times 10^{10})^{2}}{10^{16}} = 2.25 \times 10^{4} {cm}^{- 3}$

So, even though I flooded the material with electrons, there are still some holes-just a lot fewer.

Key Takeaways

The law of mass action is a cornerstone of semiconductor physics, linking electrons and holes in a simple, powerful equation.
It applies to both pure and doped semiconductors, as long as the temperature is constant and doping isn’t extreme.
This law is my go-to tool for analyzing carrier concentrations and predicting the behavior of electronic devices.

Understanding this law makes the complex world of semiconductors a lot more manageable. It’s one of those principles that, once you get it, you’ll use it everywhere in electronics.