Key Takeaways:
- Two main methods exist for converting decimal numbers to binary: the sum-of-powers method and the division-by-two method.
- The division-by-two method is the most widely used and reliable for both integer and fractional decimal numbers.
- Practice with decimal to binary questions and review decimal to binary conversion examples to reinforce your understanding.
Table of Contents
Introduction
When I first started learning about number systems, decimal to binary questions always seemed a bit daunting. But as I explored the processes, I realized it’s not as complicated as it looks—especially once you get the hang of the core methods.
If you’re just getting started or need a refresher, this guide will walk you through the main approaches, provide decimal to binary conversion examples, and offer some practice problems.
Understanding the Basics
Before diving into the methods, it’s important to clarify what decimal and binary actually mean. The decimal system is based on powers of 10, using digits 0–9. The binary system, on the other hand, works with just two digits—0 and 1—and is based on powers of 2.
Why convert decimal to binary?
Binary is the foundation of all digital systems, from computers to smartphones. Understanding decimal to binary by division and other methods is essential for anyone interested in computing, programming, or electronics.
Method 1: Sum of Powers of Two
Let’s start with the sum-of-powers method, which is intuitive but not always the quickest for larger numbers.
How it works:
You break down a decimal number into the sum of the largest possible powers of 2 (starting from the highest possible power). Each power corresponds to a binary digit.
Example: Convert 13 to binary
- List powers of 2: 8 (2³), 4 (2²), 2 (2¹), 1 (2⁰)
- 13 = 8 + 4 + 1
- Assign binary digits:
- 8 (2³): 1
- 4 (2²): 1
- 2 (2¹): 0
- 1 (2⁰): 1
- Binary result: 1101
This method is great for small numbers or for understanding the relationship between binary and decimal, but for larger numbers, it can be tedious.
Method 2: Division by Two (Preferred Method)
The decimal to binary by division method is the standard approach for converting any decimal number (including those with fractional parts) to binary.
Step-by-Step Guide for Integers
- Divide the number by 2.
- Record the remainder (0 or 1).
- Repeat with the quotient until it becomes 0.
- Write the remainders in reverse order (from last to first).
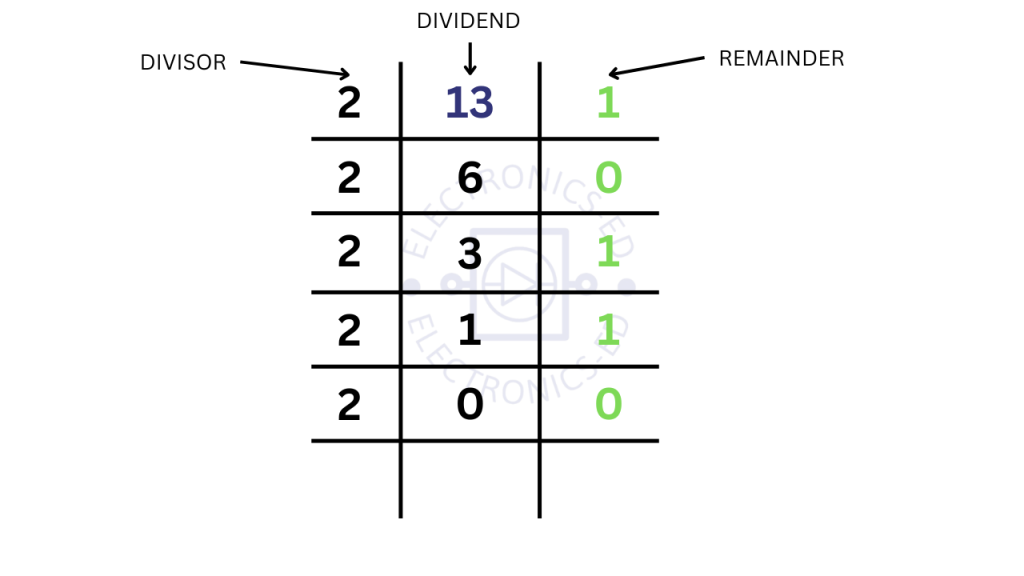
Example: 13 again
| Step | Division | Quotient | Remainder |
|---|---|---|---|
| 1 | 13 ÷ 2 | 6 | 1 |
| 2 | 6 ÷ 2 | 3 | 0 |
| 3 | 3 ÷ 2 | 1 | 1 |
| 4 | 1 ÷ 2 | 0 | 1 |
Remainders (from last to first): 1 1 0 1
Binary result: 1101
Handling Fractions
For numbers with a fractional part, you:
- Convert the integer part as above.
- For the fractional part, multiply by 2 and record the integer part of the result.
- Repeat with the new fractional part until it becomes 0 (or reaches desired precision).
- Write the integer parts in order (first to last).
Example: 25.625
- Integer part: 25 → 11001
- Fractional part: 0.625
| Step | Multiply by 2 | Integer Part | Fractional Part |
|---|---|---|---|
| 1 | 0.625 × 2 | 1 | 0.25 |
| 2 | 0.25 × 2 | 0 | 0.5 |
| 3 | 0.5 × 2 | 1 | 0.0 |
Fractional binary: 101
Final binary: 11001.101
Decimal to Binary Conversion Examples
Let’s look at a few more decimal to binary conversion examples to solidify your understanding.
Example 1: 6
- 6 ÷ 2 = 3, remainder 0
- 3 ÷ 2 = 1, remainder 1
- 1 ÷ 2 = 0, remainder 1
- Binary: 110
Example 2: 29
- 29 ÷ 2 = 14, remainder 1
- 14 ÷ 2 = 7, remainder 0
- 7 ÷ 2 = 3, remainder 1
- 3 ÷ 2 = 1, remainder 1
- 1 ÷ 2 = 0, remainder 1
- Binary: 11101
Example 3: 67
- 67 ÷ 2 = 33, remainder 1
- 33 ÷ 2 = 16, remainder 1
- 16 ÷ 2 = 8, remainder 0
- 8 ÷ 2 = 4, remainder 0
- 4 ÷ 2 = 2, remainder 0
- 2 ÷ 2 = 1, remainder 0
- 1 ÷ 2 = 0, remainder 1
- Binary: 1000011
Practice with Decimal to Binary Questions
To really master decimal to binary questions, try converting these numbers yourself:
- 18
- 47
- 128
- 29.75 (hint: convert integer and fractional parts separately)
For 29.75:
- Integer part (29): 11101
- Fractional part (0.75):
- 0.75 × 2 = 1.5 → 1
- 0.5 × 2 = 1.0 → 1
- Binary: 11101.11
Common Mistakes and Tips
- Forgetting to reverse the order of remainders for the integer part.
- Not stopping when the quotient is 0 (for integer part).
- Mixing up the order for fractional parts (should be top to bottom, not reversed).
- Ignoring leading or trailing zeros in the fractional part.
FAQs: Decimal to Binary Conversion
Q: Why do we divide by 2 to convert decimal to binary?
A: Because binary is base 2, dividing by 2 and tracking remainders efficiently captures the binary digits.
Q: How do you handle decimal numbers with fractions in binary conversion?
A: Convert the integer part by division, and the fractional part by repeated multiplication by 2.
Q: What is the fastest method for converting large decimal numbers to binary?
A: The decimal to binary by division method is generally the fastest and most reliable.
Q: Can you convert any decimal number to binary?
A: Yes, but for numbers with infinite fractional parts, you may need to decide on a level of precision.
Q: Why are there two different methods for decimal to binary conversion?
A: The sum-of-powers method is intuitive for small numbers, while the division method is more efficient and works for all numbers.
Summary Table
| Method | Best For | Steps Involved | Example Result |
|---|---|---|---|
| Sum of Powers | Small numbers | Break down into powers of 2 | 13 → 1101 |
| Division by Two | All numbers | Divide by 2, record remainder | 25.625 → 11001.101 |
Final Thoughts
Mastering decimal to binary conversion examples and practicing decimal to binary questions is a foundational skill in computing. The decimal to binary by division method is your best friend for accuracy and efficiency. Whether you’re preparing for exams or just curious about how computers work, these techniques will serve you well.
Remember:
- Use the division method for reliability.
- Practice with both integer and fractional numbers.
- Check your work by converting binary results back to decimal.